√100以上 直角 三角形 三 ��方 の 定理 449772

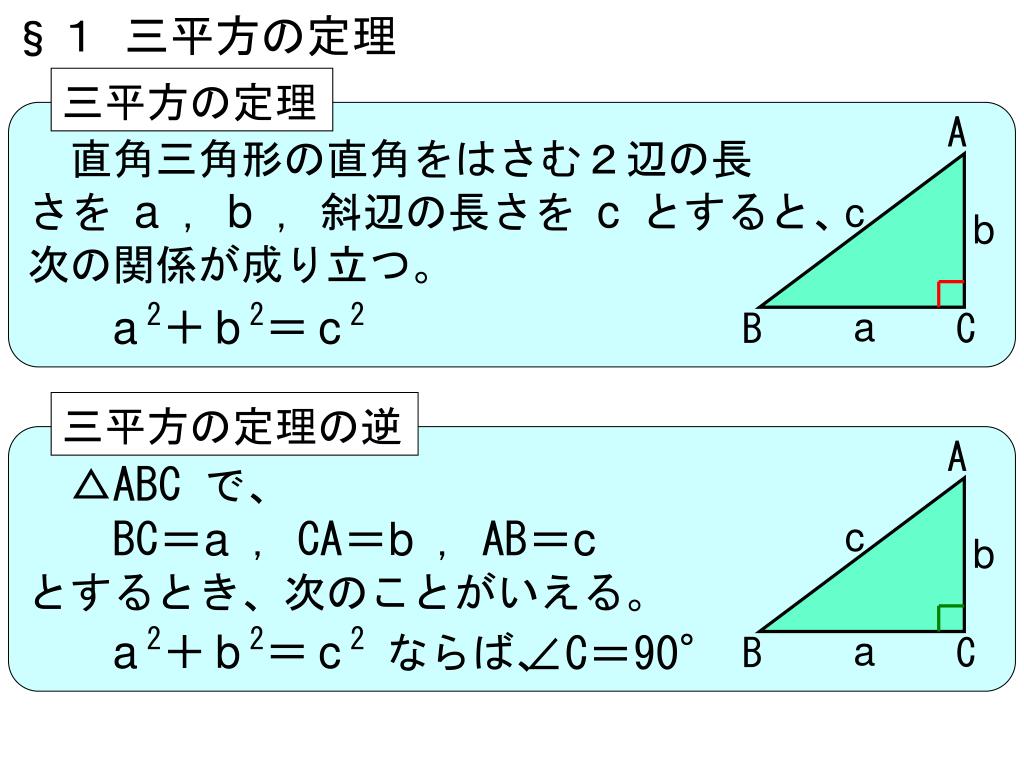
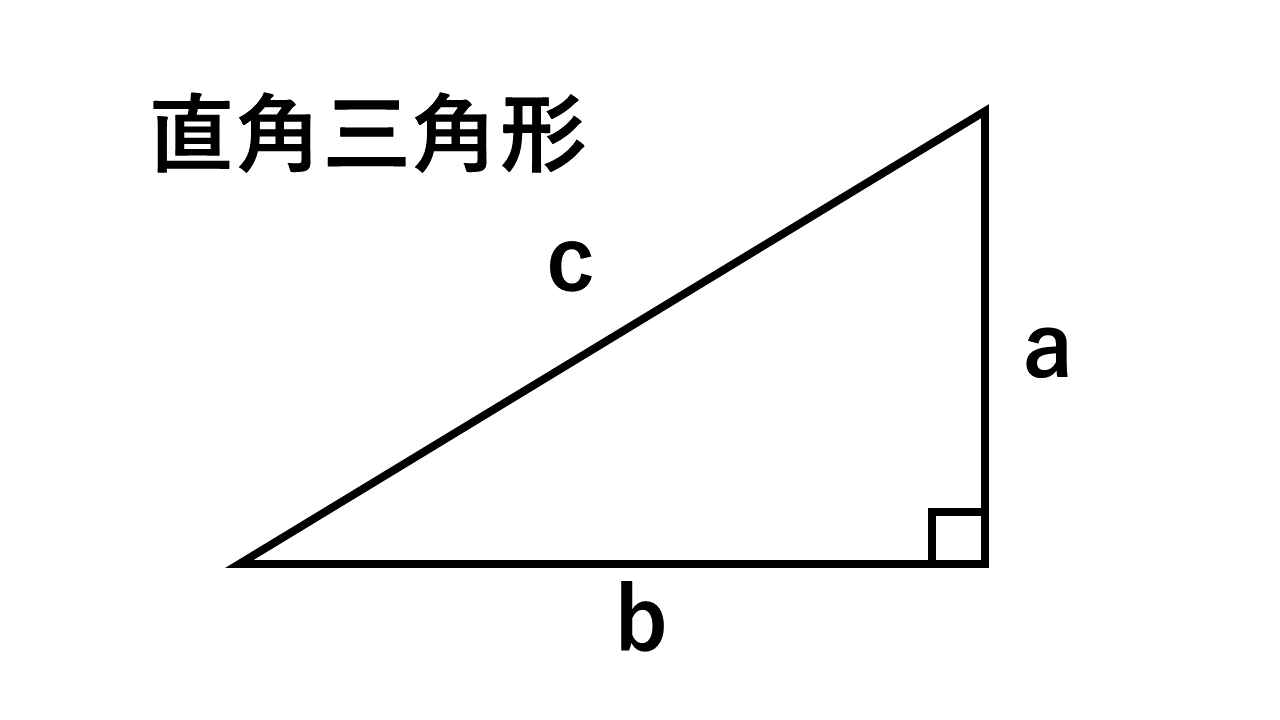
三平方の定理 ピタゴラスの定理

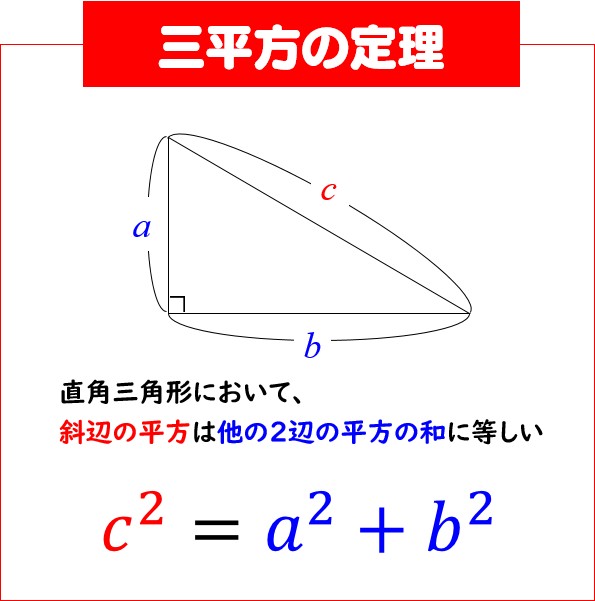
6 、三角形任意两边之和大于第三边，任意两边之差小于第三边。 7、 在一个直角三角形中，若一个角等于30度，则30度角所对的直角边是斜边的一半。 8、直角三角形的两条直角边的平方和等于斜边的平方。 9、直角三角形斜边的中线等于斜边的一半。 中学受験ですので、三辺の 辺の比が整数となる直角三角形 がよく出題されます。 左側の $\textcolor{red}{345}$ の 三角形 は 超頻出 なので、覚えておいて欲しいですが、他の2つは そんなのもあるんだぁ~ 程度で良いかなぁ と 思います。

直角 三角形 三 平方 の 定理

直角 三角形 三 平方 の 定理-直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺（高さ）の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11＝2 ⇒ 斜辺=√2」になります。 三平方の定理を使って面積を求める方法は？ 問題を使って解説するよ！ 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に

Ppt ６ 三平方の定理 Powerpoint Presentation Free Download Id

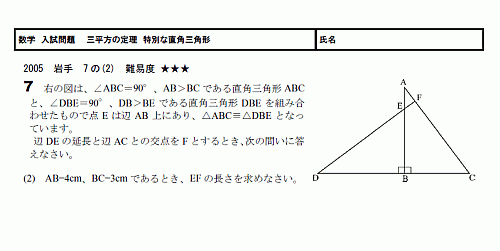
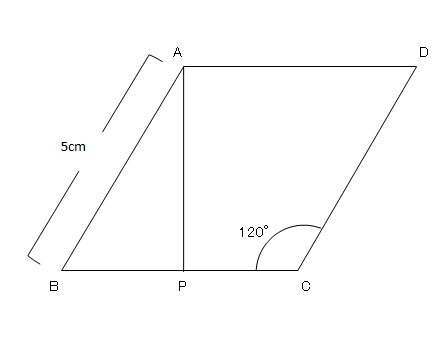
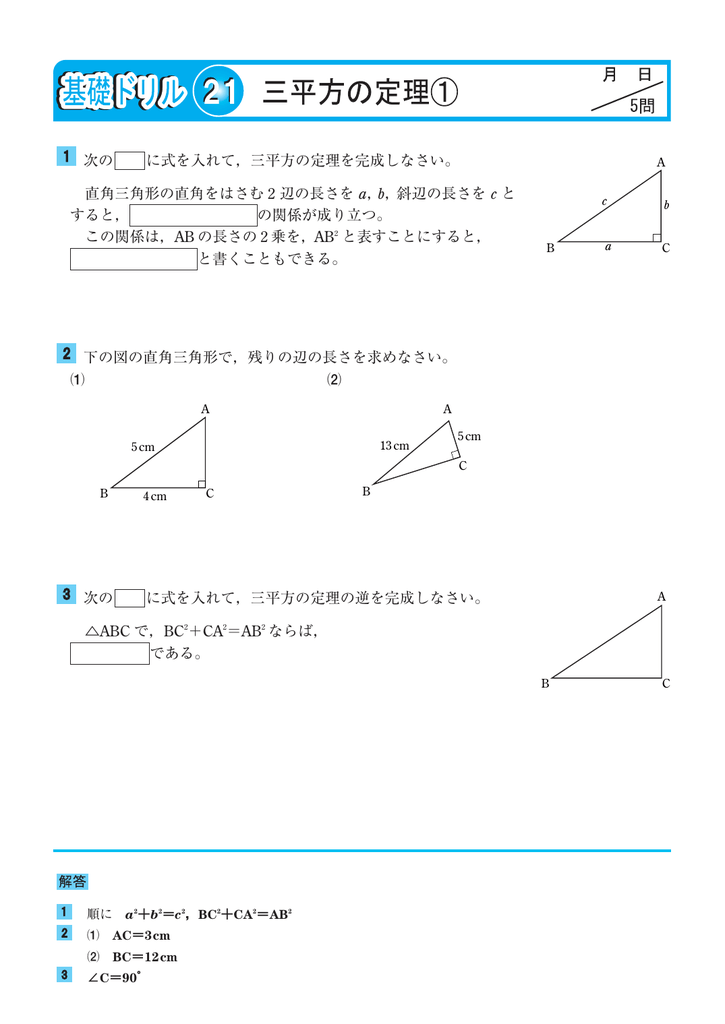
三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_2点間の距離 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離では直角三角形を図にしていきましょう。 sinは高さ/斜辺 なので、直角三角形の 高さ5,斜辺13 とわかります。 底辺は、 三平方の定理 を使えば、 a 2 b 2 =c 2 5 2 底辺 2 =13 2 底辺=12 とわかります。 四平方の定理三平方の定理というと, 直角三角形において,(斜辺の2乗) = (他の2辺の2乗の和)が成り立つという有名な定理ですここでは, 三平方の定理(平面上の定理)を3次元に拡張した, 四平方の定理を紹介します 定理 3つの面が直角三角形で, 1つの頂点に直角が集まっている三角錐を考え

三角定規型 暗記しておくべき直角三角形があります。 それは三角定規の形です。 三角定規は \(2\) 種類あります。 その \(2\) 種類は必ず暗記すべき特別な直角三角形です。 45° 45° 90° まずはじめに直角 愛 の ため に for love for a child one; この三角形が直角三角形 ⇔ a2 b2 = c2 a 2 b 2 = c 2 三平方の定理から, 辺の長さが整数である直角三角形を見つけることは, a2 b2 = c2 a 2 b 2 = c 2 を満たすような整数 (a,b,c) ( a, b, c) の組を見つけることと同じになります

直角 三角形 三 平方 の 定理のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	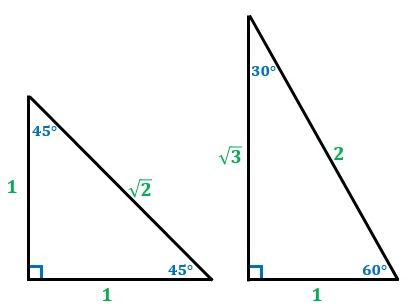三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	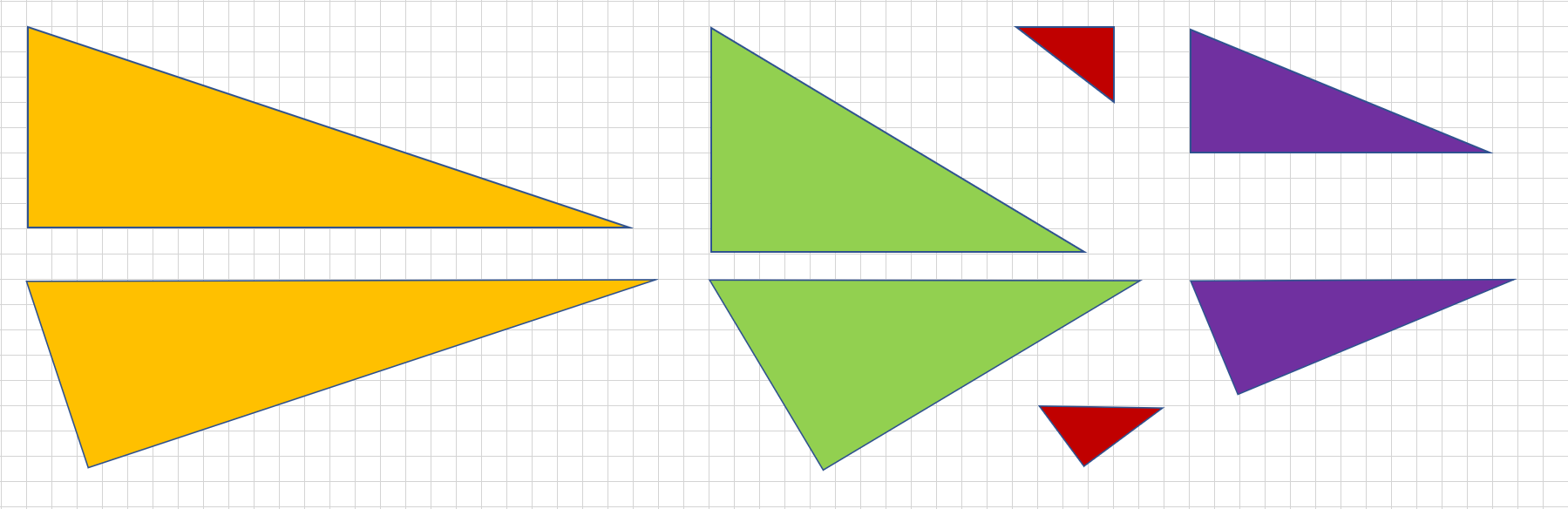三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
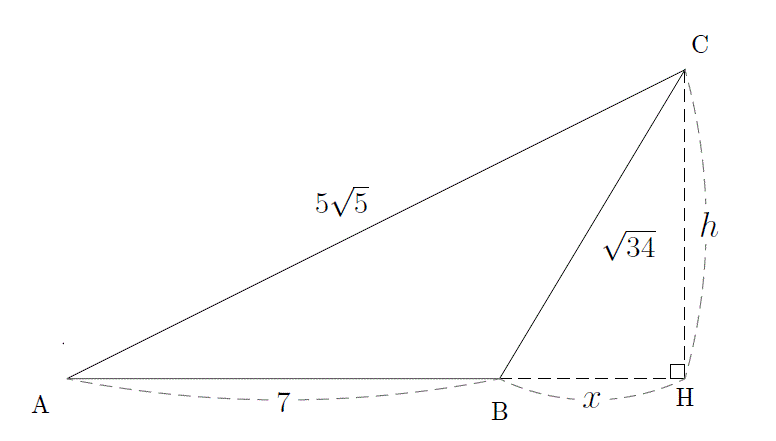三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	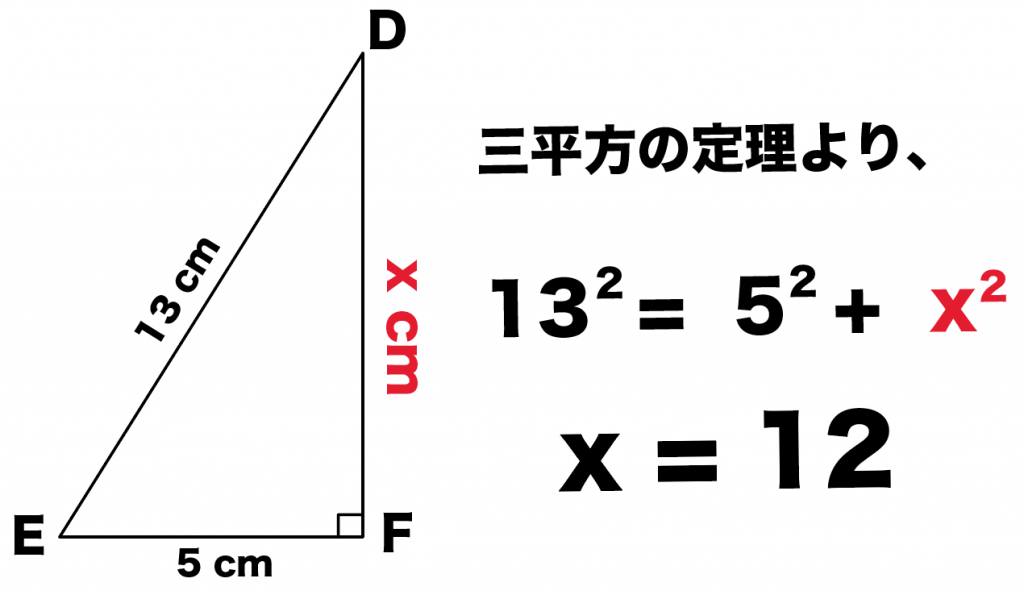三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	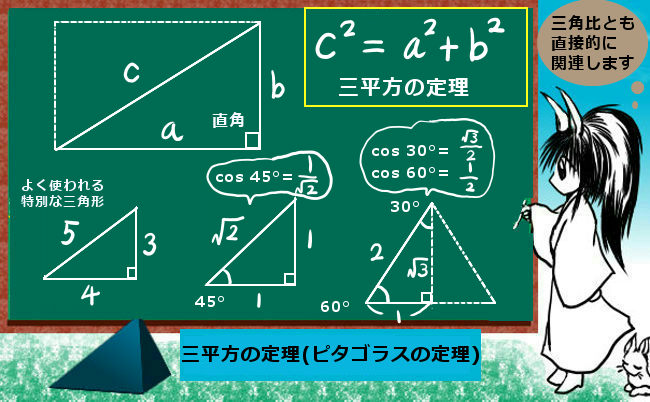三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	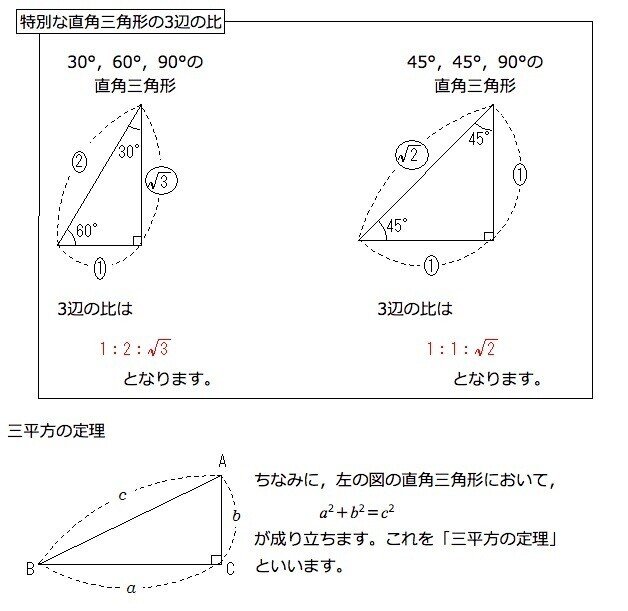三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	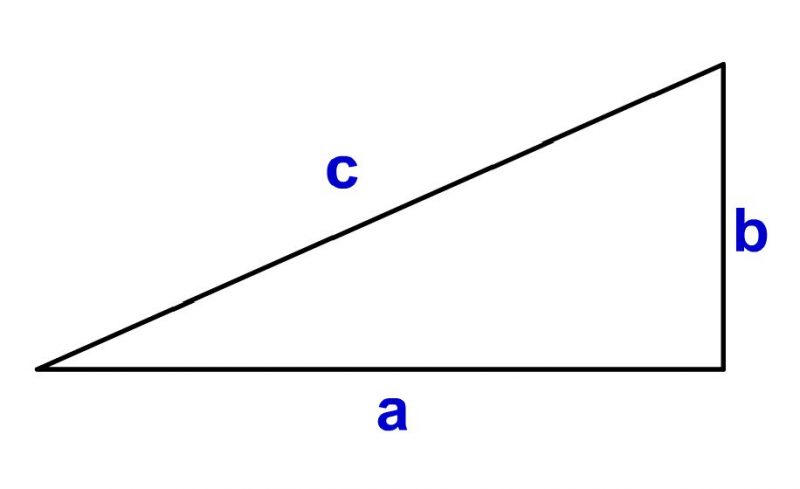三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	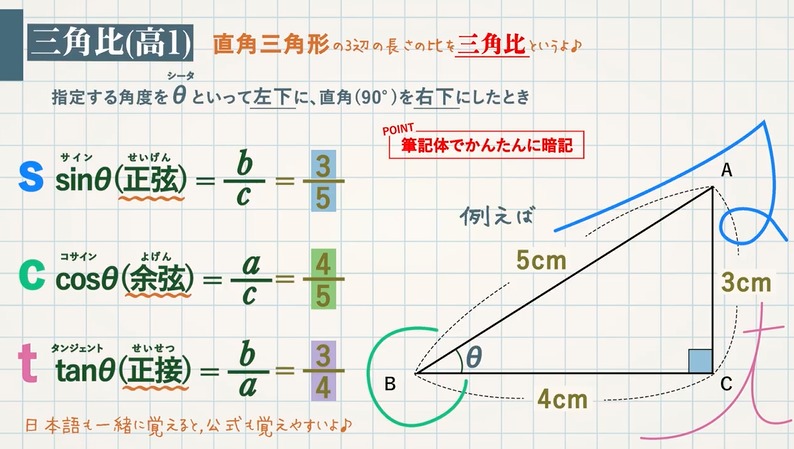三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	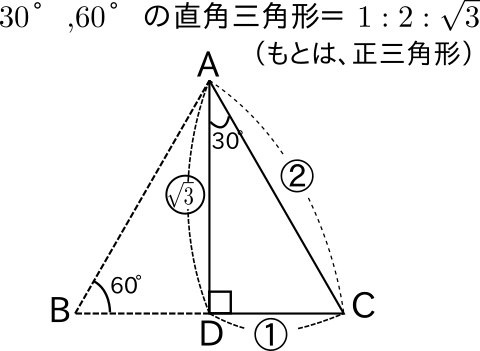三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学	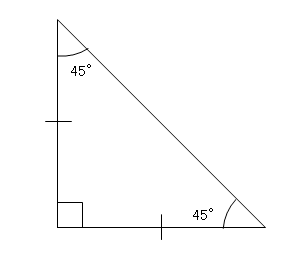三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学

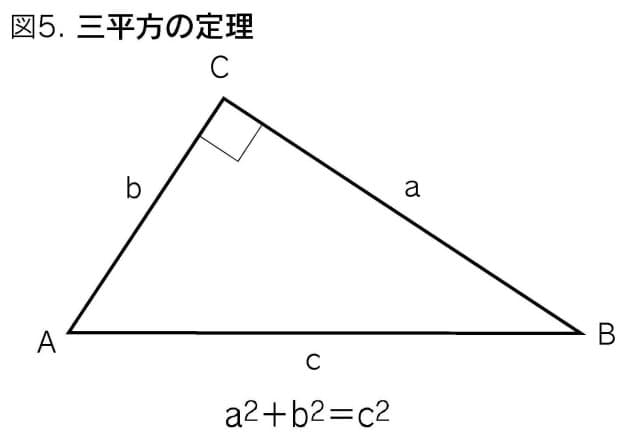
 3：4：5の三角形で，本当に直角ができるのでしょうか。 三角形の辺の長さの比と角の大きさには，どんな関係があるのでしょうか。 3：4：5は，斜辺の対角が直角です。このことは，三平方の定理として知られています。 3：4：5が成り立つとき，その三角形は直角三角形です． （これを三平方の定理の逆といいます．） 一番長い辺が斜辺です． ※ 直角三角形であるかどうかを調べるには， a 2 b 2 と c 2 を比較してみれば分かります． 例 三辺の長さが 3,4,5 の三角形が直角三角形